The paper “Big algebras” is in the arxiv. Here is the abstract:
“Here we announce the construction and properties of a big commutative subalgebra of the Kirillov algebra attached to a finite dimensional irreducible representation of a complex semisimple Lie group. They are commutative finite flat algebras over the cohomology of the classifying space of the group. They are isomorphic with the equivariant intersection cohomology of affine Schubert varieties, endowing them with a new ring structure. Study of the finer aspects of the structure of the big algebras will also furnish the stalks of the intersection cohomology with ring structure, thus ringifying Lusztig’s q-weight multiplicity polynomials i.e. affine Kazhdan-Lusztig polynomials.”
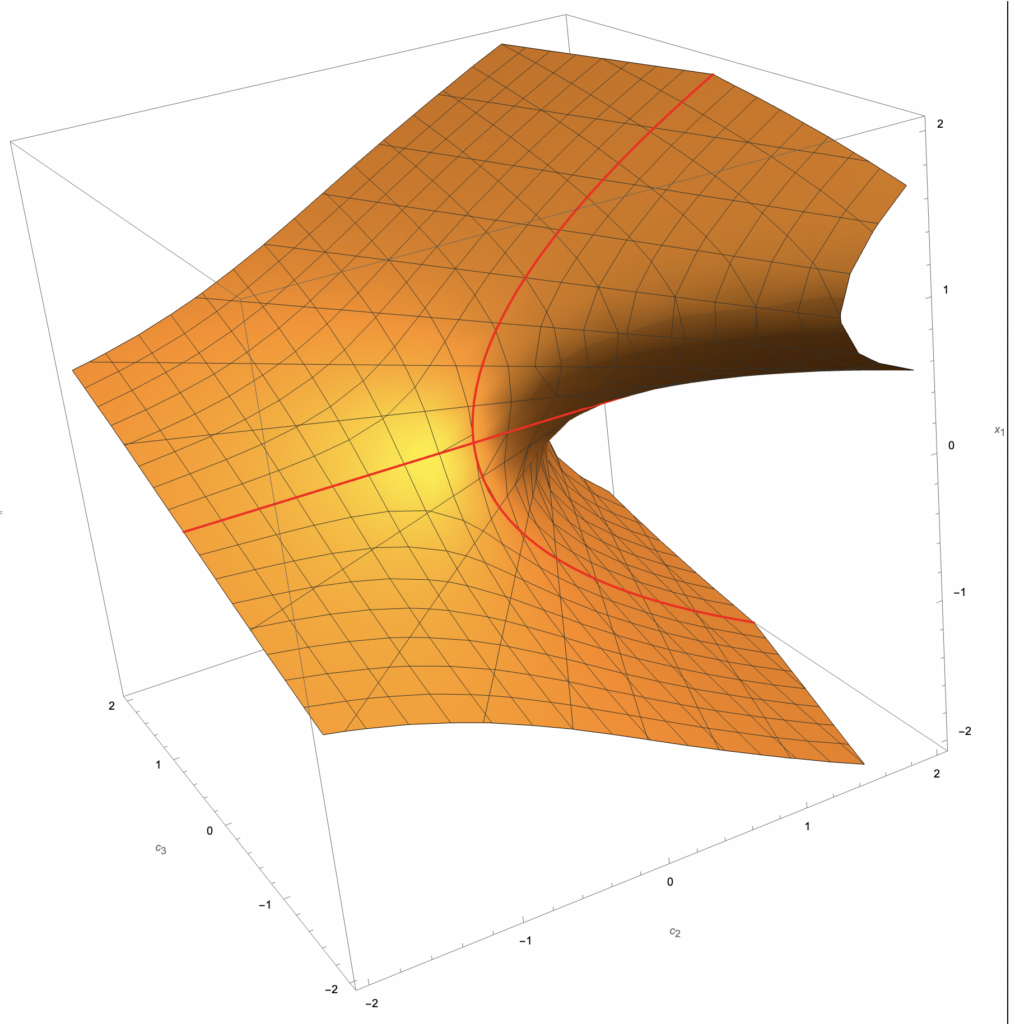
Here is the big zero scheme of the standard representation of SL(3) branched to the principal SL(2) subgroup (c.f. Theorem 4.2):
(originally from paper)